Inequações do 1º e do 2º grau

Vamos resolver hoje alguns exercícios de inequações. Pelo o que eu vejo em muitos lugares as inequações chegam a confundir muitas pessoas, mas vou mostrar a vocês que não é preciso entrar em pânico.

Em primeiro lugar vamos aprender a estudar o sinal de determinados gráficos:

Função do 1º grau:

• a > 0

Observamos que depois do x o f(x) será positivo, e que antes do x o f(x) será negativo.

• a < 0

Observamos que antes do x o f(x) > 0 e depois do x o f(x) é < 0.

Função do 2º grau:

• a > 0

Observamos que entre as raizes x1 e x2 o f(x) < 0, e também que antes do x1 e depois do x2 o f(x) > 0

• a < 0

Observamos que entre as raízes x1 e x2 o f(x) > 0, e que antes do x1 e depois do x2 o valor de f(x) < 0.

No que esse estudo de sinais vai nos ajudar?

Simples! Em tudo.

Em uma inequação teremos que achar o valor de x que satisfaz determinadas condições.

Por exemplo:

x² + 2 > 0

(x + 1) . ( x + 2)  ≥  0

(x + 2) . ( - x + 1) / (2x + 1) ≤ 0

E para saber quais os valores que são menores ou iguais a zero basta fazer o estudo de sinais.

Vamos fazer exercícios para que essa ideia fique clara:

Exercicios:

1- Resolva a inequação:

(x - 1) . (x + 2)  ≥ 0

Vamos fazer a raíz de (x - 1) e ( x + 2) e estudar os seus sinais:

Há algo chamado "varal dos sinais", nele você colocará as raízes, e os sinais que estão antes e depois delas, observe:

O que eu fiz passo-a-passo:
I - Observe o estudo dos sinais, percebemos que antes do -2 era sinai negativo, e depois dele sinal positivo. E também pudemos observar que antes do 1 era negativo, e depois dele era positivo.
II - Tendo esses dois estudos, vamos juntar ambos e formar apenas um varal, que será o definitivo.

• Antes do -2 temos dois sinais negativos (-) e (-), sabemos que menos com menos dá positivo, por isso o sinal positivo antes do -2.
• Entre -2 e 1 temos dois sinais, um deles positivo e o outro negativo (+) e (-), sabemos que mais com menos, dá sinal negativo, por isso o sinal entre -2 e 1 é negativo.
• Depois do 1 temos dois sinais positivos (+) e (+), sabemos que mais com mais, da sinais positivo. Por isso depois do 1 temos um sinal positivo.

III - Vamos ver o que o nosso enunciado deseja:
(x - 1) . (x + 2)  ≥ 0

Ele quer os valores de x que dê MAIOR ou IGUAL a zero.

Vendo no varal quais valores são positivos e igualam a zero (as raízes), temos valido:
Antes do -2
Depois do 1

Como pode ser IGUAL a zero, as raízes também entraram no nosso valor, por isso utilizamos BOLINHA FECHADA, certo?

Resposta:

S = {x e R/ x ≤ -2 ou x  ≥ 1} 

Outra maneira de dar a resposta é:

S = ] - ∞; -2] U [1; + ∞[

U (lembre-se que é o símbolo da união)



2- Resolva a inequação:

(x + 2).(-x + 1) ≤ 0
      (2x  - 1)


Vamos analisar as raízes:

Vamos agora montar o "varal dos sinais": (sempre colocando em ordem crescente)

Como o enunciado do exercício pede os valores ≤ 0, temos como resposta:

S = { x e R/ -2 ≤ x < 1/2 ou  ≥ 1}

Outra maneira:

S = [-2; 1/2[ U [1; + ∞[


OBS: O 1/2 apresenta bolinha aberta, porque sabemos que o seu resultado deve ser diferente de zero, já que não podemos dividir um número por zero. Caso coloquemos 1/2 como resultado possível, isso significa que iremos anular (2x -1) e vamos estar fazendo uma divisão por zero, que nesse caso é inadmissível. 


3- Resolva a inequação:
x² + x + 3 > x
 x   +  1


Em primeiro lugar vamos "arrumar" essa equação:

x² + x + 3   - x  > 0
   x + 1

Faremos o mmc:

x² + x + 3 - x(x + 1)  > 0
         x + 1


x² + x + 3 - x² - x  > 0
        x + 1 


Teremos então:

   3     > 0 
x + 1 


Nesse caso teremos que avaliar apenas uma raíz:

Como o enunciado deseja apenas > 0, teremos como resposta:

S = {x e R/ x > -1}

Outra maneira de responder:

S = ]-1; + ∞[


Vamos fazer uma do segundo grau agora para termos como exemplo:

4 - Resolva a inequação:
3x² + 10x + 7 < 0

Descobrindo as raízes, basta igualar a zero e fazer bhaskara:

Delta: 10² - 4(3)(7) 
Delta: 100 - 84
Delta: 16

x = -10 +- 4/ 6

x1 = -10 + 4/6 = -1
x2 = -10 - 4/6 = -7/3


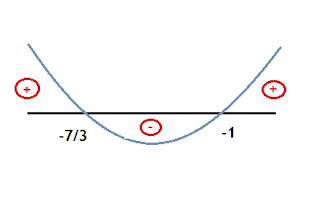
Fazendo estudo dos sinais:

Os valores que satisfazem o que o nosso enunciado pede "< 0" são:

S = {x e R/ -7/3 < x < -1}

Nesse caso ambos são bolinha aberta por causa do sinal "<"

Outra maneira de responder:

S = ]-7/3; -1[




Uma dica para saber se é bolinha aberta ou bolinha fechada é:

• Caso tenha  ≥ ou ≤, é BOLINHA FECHADA
• Caso tenha > ou <, é BOLINHA ABERTA

Nota:

Espero que esse post tenha sido útil, qualquer dúvida, deixo os comentários abertos para dúvidas, sugestões ou qualquer outro comentário que vocês desejem fazer!

Caso queiram deixo aqui o nosso e-mail: entendaexatas@hotmail.com

Não se esqueçam que estamos aqui para auxiliar vocês!